Pandiagonale magische Quadrate

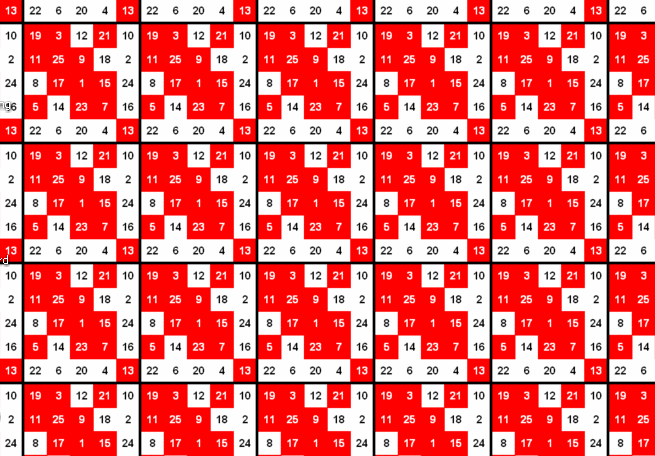
Sind die Summen der Zellen in den gebrochenen Diagonalen ebenfalls magisch, wird die Matrix als pandiagonales magisches Quadrat oder Teufelsquadrat bezeichnet. Ordnet man viele pandiagonale magische Quadrate der Ordnung n zu einer Tapete an, so ist jedes beliebig entnommene n×n-Quadrat magisch.

Ein pandiagonales magisches Quadrat kann man sich auch als Torus vorstellen. Er entsteht, wenn man das Quadrat zu einer Rolle einrollt und die Rolle zu einem Ring.

4×4 pandiagonales magisches Quadrat

Magische Summe = 34

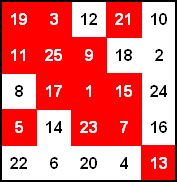
5×5 pandiagonales magisches Quadrat

Magische Summe = 65. Die Summen der Zellen in den gebrochenen Diagonalen ergeben ebenfalls die magische Summe.

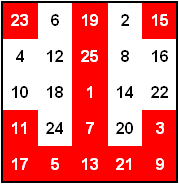
6×6 pandiagonales magisches Quadrat

Magische Summe = 246. Besitzt nicht aufeinander folgende Zahlen. Ist ein Teilquadrat eines 9×9 Quadrates.

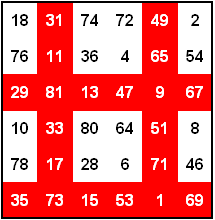
7×7 pandiagonales magisches Quadrat

Magische Summe = 175

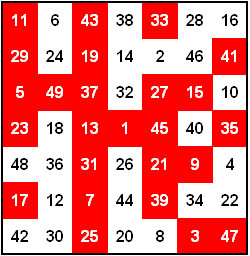
8×8 pandiagonales magisches Quadrat

Magische Summe = 260

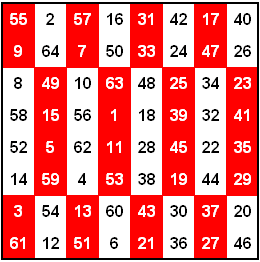
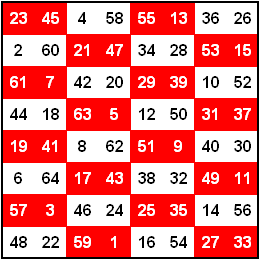
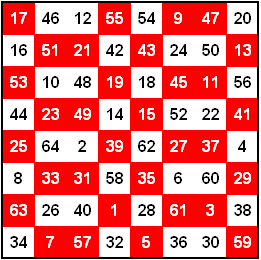
9×9 pandiagonales magisches Quadrat

Magische Summe = 369. Enthält Finale 1.

12×12 pandiagonales magisches Quadrat

Magische Summe = 870